Can you match the MEPs with their Member States? http://www.thinkingabout.eu/match
venerdì 15 aprile 2016
Pubblicato da
koteth
0
commenti
![]()
Etichette: eu, european parliament, european union, game, javascript, mep, phaser.js
martedì 24 maggio 2011
A method to exchange keys and values in a python dictionary
Around the web i've found this method to exchange keys and values in a python dictionary:
the_dict = { 'a': 1, 'b': 2, 'c': 3 }
inverted_dict = dict(zip(*zip(*the_dict.items())[::-1]))
output:
{ 1:'a', 2:'b', 3:'c' }
it is nice isn't it?
but how does it work?
The main idea is to split keys and values in a list of two n-tuples $$[ (k_1,...,k_n) , (v_1,...,v_n)] ,$$
switch the tuples and re-create a dictionary.
ingredients are:
1 - operator * (also known as 'splat' operator) that is able to unpack a list
2 - zip function that returns a list of tuples, where the i-th tuple contains the i-th element from each of the argument sequences or iterable
3 - a_list[::-1] to revert a_list
We can unpack the algorithm in those 5 nested steps:
a - the_dict.items()
b - zip(*the_dict.items()) c - zip(*the_dict.items())[::-1] d - zip(*zip(*the_dict.items())[::-1]) e - dict(zip(*zip(*the_dict.items())[::-1]))
a - with the_dict.items() we obtain:
[('a', 1), ('b', 2), ('c', 3)]
b - then, using * operator in the zip function:zip(*the_dict.items()) we are doing: zip(('a', 1), ('b', 2), ('c', 3) ) obtaining: [('a', 'b', 'c'), (1, 2, 3)]
c - with [::-1] we actually switch key and values
zip(*the_dict.items())[::-1] = [('a', 'b', 'c'), (1, 2, 3)][::-1]
=
[('a', 'b', 'c'), (1, 2, 3)]
d - with the second zip * pair we re-unpack the list to recreate the 3 pairs:
zip(*zip(*the_dict.items())[::-1]) =
zip(*[('a', 'b', 'c'), (1, 2, 3)]) =zip(('a', 'b', 'c'), (1, 2, 3) )
=
[('a', 1), ('b', 2), ('c', 3)]
e - now our new dict is almost cooked, we use dict() function to complete the opera:
dict(zip(*zip(*the_dict.items())[::-1]))
=
dict ([('a', 1), ('b', 2), ('c', 3)])the output:{ 1:'a', 2:'b', 3:'c' }all this stuff in 1 row.
Pubblicato da
koteth
1 commenti
![]()
lunedì 23 maggio 2011
Happy numbers in python
I'll show you a method in python to check if a number is happy.
When a number is happy? Well, you have to follow this algorithm:
1. Take a number n.
n = 23
2. Dissect it into digits.
2 and 3
3. Square them all and add them up
2^ 2 + 3 ^ 2 = 4 + 9 = 13
4. You get a new number m.
m = 13
5. If m = 1, n is happy; otherwise set n = m and repeat at 1.
1^2 + 3^2 = 1 + 9 = 10
n = 10
1 ^ 2 + 0 ^ 2 = 1
23 is happy!
6. If you run into a loop, n is not a happy number (is sad).
I've used recursion because it is fun (talking about happy numbers).
def happy(n, past = set()): m = sum(int(i)**2 for i in str(n)) if m == 1: return True if m in past: return False past.add(m) return happy(m,past) print [ x for x in range(1,100) if happy(x, set())]
Here 'past' is a set, needed to check if we are in a loop.
The output shows the set of happy numbers below 100.
[1, 7, 10, 13, 19, 23, 28, 31, 32, 44, 49, 68, 70, 79, 82, 86, 91, 94, 97]
Pubblicato da
koteth
0
commenti
![]()
giovedì 19 maggio 2011
logistic map in python
Simple logistic map using python and matplotlib.
import math
import matplotlib.pyplot as plt
def logistic(xa =2.9 , xb=4.0 , imgx = 240 , imgy = 500,
maxit = 200, f=lambda x,r: r * x * (1 - x) ):
xs = []
ys = []
for i in range(imgx):
r = xa + (xb - xa) * float(i)/(imgx - 1)
x = 0.5
for j in range(maxit):
x = f(x,r)
if j > maxit / 2:
xs.append( i )
ys.append(int(x * imgy))
return [xs,ys]
myfunction = lambda x,r: r * (math.sin(x)**2)
points = logistic( xa = 2.1 ,xb = 3.1, imgy=200 , f=myfunction)
ax = plt.subplot(121)
ax.scatter(points[0], points[1], s= 1)
points = logistic()
bx = plt.subplot(122)
bx.scatter(points[0], points[1], s= 1)
plt.show()
Pubblicato da
koteth
0
commenti
![]()
Etichette: chaos, math, matplotlib, python
lunedì 4 aprile 2011
Caostabile is Online
A little bit of Math and Physics curiosities and amenities ( in italian ) .
http://caostabile.altervista.org/
Pubblicato da
koteth
0
commenti
![]()
martedì 3 agosto 2010
venerdì 26 marzo 2010
Similarity Matrix in Text Mining
What is a similarity matrix ( in text mining ) and why is important?
CORPUS
We have to start from a corpus composed by k documents:
SIMILARITY MATRIX
A way to find semantic structures in the corpus is to study the occurrence and the
co-occurrence for every pair of words in the corpus.
A good tool to find something interesting is a similarity matrix.
DEFINITION
To define a similarity matrix we must define the similarity between two objects ( words )
the objects of index i and j for the generic position {i,j}
a good similarity matrix can follow from this definition: $$ s(w_i,w_j) = \dfrac {c(w_i,w_j) } { f(w_i) \cdot f(w_j) }$$ where: $$ c(w_i,w_j) $$ is the co-occurrence between two words ( the number of documents containing both
words )
MATRIX REPRESENTATIONS
- GRAPH
The created matrix is symmetric and could be visualized using a undirected weighted graph.
The nodes represents the words and the similarity between the two words is given by the
weight between two nodes.
this visualization is nearly useless (easily more than 10000 nodes!!!) .
- METRIC SPACE
A way to handle this info is to position k points in an n-dimensional space so that the mutual
distance between a couple of elements previously defined could reflect the weight between
the related pair of words.$$w_i \mapsto p_i | s(w_i,w_j) = \dfrac{1}{||p_i - p_j||} \forall i,j \leq k$$
( higher weight - closer distance )
a problem related with this approach is that is not always operable (matrix could not be
compatible with metrics constraints ) and the requested dimension of the target space
is a $$O(k^2).$$
so we need to use a technique to reduce the dimension preserving the significant information
( reducing the dimension brings a certain loss of information).
SEMANTIC STRUCTURES
Using the representation in an n-dimensional space is important to analyze clusters of points.
A cluster could be defined as a subset of points whose mutual distances are much smaller
than the average distance of the complete set.
A cluster is a reflection of some kind of statistical structure of the corpus.
Structures able to create a cluster can either be:
- language related rules ( eg: syntactic structures ) or
- semantic meanings ( eg: topics )
Pubblicato da
koteth
0
commenti
![]()
Etichette: data mining, math, text mining
martedì 29 dicembre 2009
Verlet integration in Haskell
Pubblicato da
koteth
2
commenti
![]()
giovedì 24 dicembre 2009
my delicious
Pubblicato da
koteth
1 commenti
![]()
martedì 8 dicembre 2009
Cairo-Chaos Haskell

Haskell chaos and lib-cairo.
Is only a fixed-point iteration over this function:
lgs x r = r * x * exp(- x )
Pubblicato da
koteth
0
commenti
![]()
Dollar $ operator in Haskell
Do you know what is $ operator in Haskell?
$ means simply , 'apply the left function at the right value'.
f $ x := f x
it seems really trivial, isn't it ?
But, for example in this kind of situation, is really usefull:
zipWith ( $ ) ( cycle [ \x -> div (x + 1) 2 , \x -> div x 2 ] ) [1..]
here you have a infinite list of function:
a = cycle [ \x -> div (x + 1) 2 , \x -> div x 2 ]
( ie: [\x -> div (x + 1) 2 , \x -> div x 2 , \x -> div (x + 1) 2 , \x -> div x 2, ... ] )
and you want to apply every element of the list at the element
at the same index in the second list:
b = [1..]
zipWith, for every index i takes the element a(i) of the left list
and b(i) of the right list and execute what is requested inside the parentheses.
In this situation is specified $ so:
a(i) $ b(i ) := a(i) ( b(i) )
the result must be the following:
[ 1 ,1 , 2, 2 , 3 ,3 ... and so on.
Pubblicato da
koteth
0
commenti
![]()
Prime Numbers in haskell
well, do you want to know how to find 'prime numbers' in a quick and dirty
way using Haskell ?
try this!
import Data.List
nubBy ( \x y -> mod y x == 0 ) [2..]
Haskell is so easy and charming...
( ps: if you want to speed up a little bit:
nubBy ( \x y -> ( x*x-1 <= y ) && ( mod y x == 0 ) ) [2..]
)
Pubblicato da
koteth
1 commenti
![]()
giovedì 20 agosto 2009
re: Mandelbrot Set in Haskell
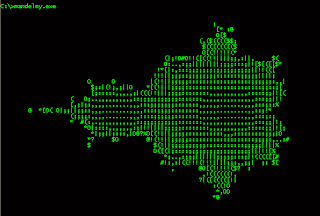
Pubblicato da
koteth
0
commenti
![]()
Mandelbrot set in Haskell
gr = map(\y-> [( x:+y )|x<-[-3,-2.95..1]])[-2,-1.9..2]
main = mapM_ putStrLn ( (map(\el->show el) )image )

A first interpretation ( a little bit unsatisfactory ) of the Mandelbrot set in Haskell
Pubblicato da
koteth
0
commenti
![]()
martedì 18 agosto 2009
Numbers in Haskell
The core of numbers post in Haskell:
numList p x = map ( idens p x ) ( map ( x * ) [ 1..( p-1 ) ] )
matIde p = map ( numList p ) [ 1..(p-1) ]
Pubblicato da
koteth
0
commenti
![]()
domenica 16 agosto 2009
The Path of St. Augustine
Pubblicato da
koteth
0
commenti
![]()
Etichette: Il Cammino di Sant'Agostino, Italy, lombardia, The Path of St. Augustine
Dungeon ( Quinta da Regaleira - Portugal )
Quinta da Regaleira
( Mystic Cristina )
Pubblicato da
koteth
0
commenti
![]()
Etichette: image
domenica 19 luglio 2009
Mandelbrot in Rebol

And this is my interpretation of Mandelbrot fractal using Rebol:
Pubblicato da
koteth
0
commenti
![]()
domenica 12 luglio 2009
Latent Semantic Indexing ( LSI )
Pubblicato da
koteth
0
commenti
![]()
Etichette: data mining, text mining
sabato 11 luglio 2009
Peano in Js
Pubblicato da
koteth
0
commenti
![]()
Etichette: image, javascript, jquery



